100次浏览 发布时间:2024-08-07 13:48:37
0.0 神说,要有正态分布,于是就有了正态分布。*
0.1 神看正态分布是好的,就让随机误差都随了正态分布。
0.2 正态分布的奇妙之处,就是许多看似随机事件竟然服从一个表达式就能表达的分布,如同上帝之手特意为之。[1]
——《创世纪·数理统计·正态分布的前世今生》
一、神觉得抛硬币是好的,于是定义每个抛出硬币正面记+1分,反面记-1分。
创世纪从0分开始,神只抛1次硬币,有2种可能:一半的概率+1分,一半的概率-1分。
此时概率分布大概是这样的:
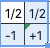
一半的概率+1分,一半的概率-1分
画图大概是这样子:
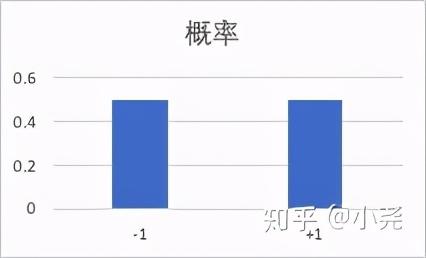
一半的概率+1分,一半的概率-1分
神决定扔10个硬币:

一样的做出概率分布
当然,同样画个图感受一下:
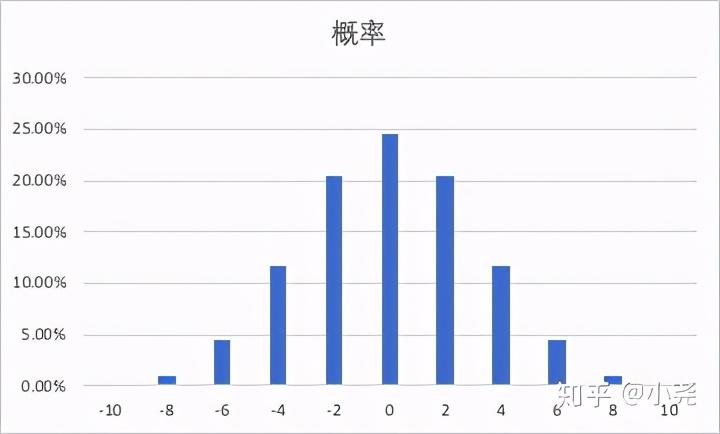
10个硬币的概率分布情况
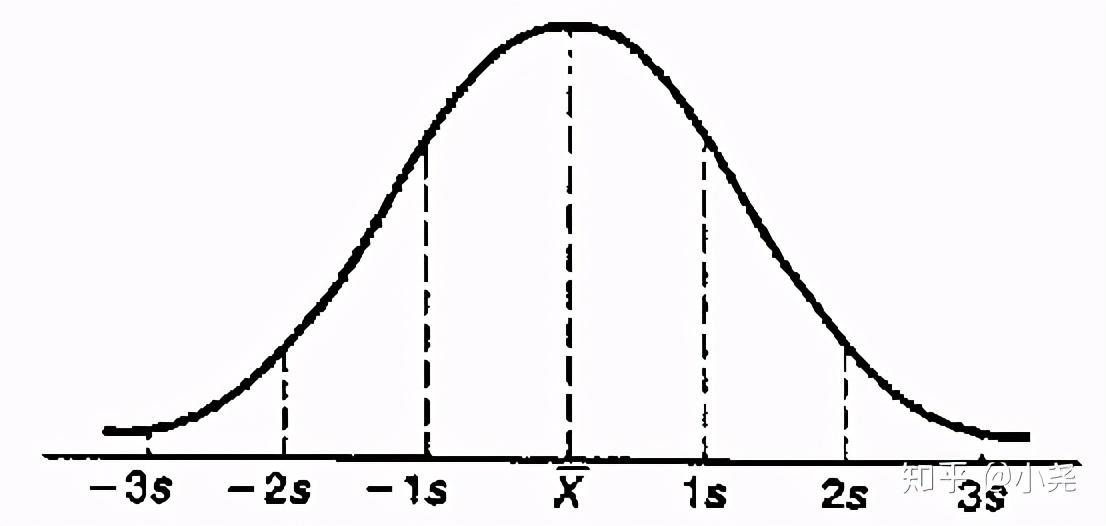
如果是100个,甚至是无穷多个呢?平均分数分布情况大概是什么样呢?画个图感受一下:
二、为什么正态分布这么常见呢?
因为通常情况下,一个事物的影响因素都是多个,比如每个人的身高,受到多个因素的影响,比如:
每一个因素,每天的行为,就像刚才抛硬币一样,这些因素要不对身高产生正面影响,要不对身高产生负面影响,最终让整体身高接近正态分布。
学过基础统计学的同学大都对正态分布非常熟悉,但是很难用通俗的语言解释什么是正态分布,主要原因是正态分布需要有一个前置知识【中心极限定理】。
如果误差可以看成许多微小量的叠加,则根据中心极限定理[1],随机误差理所当然是正态分布[2]。
正经的数学:正态分布又名高斯分布(Gaussian distribution)。
假设一随机变量X服从一个期望为 μ,方差为 σ2 的正态分布,概率密度函数为
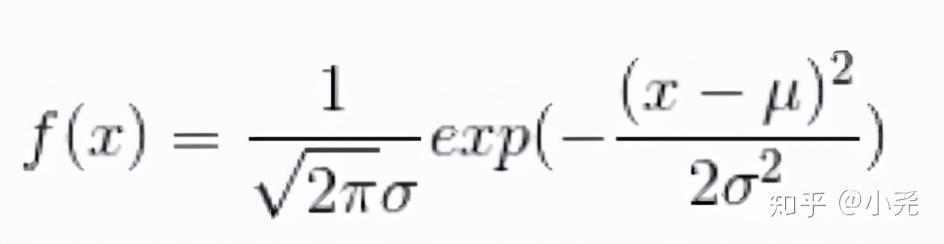
正态分布公式
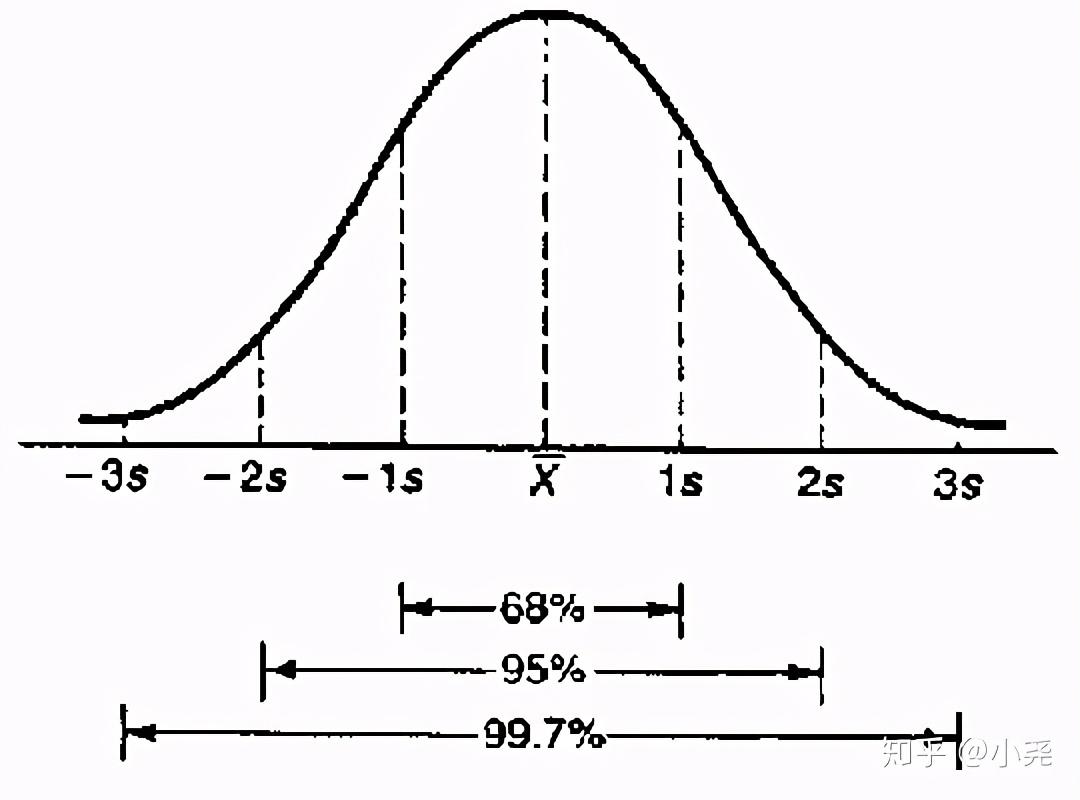
则可记为:X∼N(μ,σ2),画图如下图:
*神的名字是约翰·卡尔·弗里德里希·高斯,C.F.Gauss,1777年4月30日-1855年2月23日
[1]正态分布为什么常见?真正原因是中心极限定理(central limit theorem)。根据中心极限定理,如果一个事物受到多种因素的影响,不管每个因素本身是什么分布,它们加总后,结果的平均值就是正态分布。
[2]正态分布只适合各种因素累加的情况,如果这些因素不是彼此独立的,会互相加强影响,那么就不是正态分布了。PS:如果各种因素对结果的影响不是相加,而是相乘,那么最终结果不是正态分布,而是对数正态分布(log normal distribution)