100次浏览 发布时间:2024-08-15 13:47:53
二维曲率,二维曲率相当有趣(以后简称曲率),它和大家想象的时空曲率有所差距,却又是理解时空曲率的基础。
那么大家就开门见山地问了:那你说说,什么是二维曲率,这种曲率的意义又是什么呢?

在讲曲率是什么之前,我先带领大家看一些我们生活中常见的东西:
请看下图,你说道:这不就是两条直线嘛。
接着。我们再看这条曲线:
我相信,你此时的脑海里已经将曲率,直线,曲线这三者联系起来了。你不由自主地猜想到:“我觉得直线的曲率是0,曲线的曲率不是0。曲线曲线,自然有曲率了,而且应该不是0.”
没错,你这样想完全没问题,因为我们的逻辑几乎都是从具体到抽象的,而反过来就难以理解了,我们的大科学家们为了描述自然界中的曲直现象,因此不得不定义出某种新的概念或是发明新的数学方法来。如果我们生在他们那个知识贫瘠的年代,也一定会像他们一样,想当然地定义和运算某些新发现的事物。

高斯
请仔细看下图,曲线的弯曲程度在每个点上都是不同的!有的地方弯曲的明显感觉厉害,有的地方明显就没那么厉害了,我们想当然地会说:弯曲大的地方曲率会大,弯曲一般的地方曲率则小。

那么,大数学家高斯就说了:“我要定量分析曲率,我要自己发明描述曲率的数学工具,定义自然界曲率的数学规则,而不是定性地用“大”或者“小”描述它。”
他是怎么做的呢?我们引入曲率圆和曲率半径的概念:

曲率K用哪个公式算呢?它是由y=f(x)的一阶导数和二阶导数组合而成的公式,如果你不懂导数,请在笔者空间看讲导数的那一篇文章。
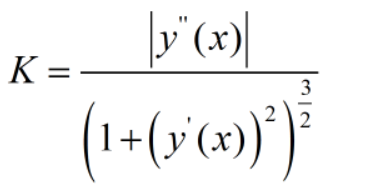
注意,我们现在研究的曲率只是二维平面的曲率,而未来要讲的三维曲率,四维曲率(黎曼曲率)一个比一个复杂。
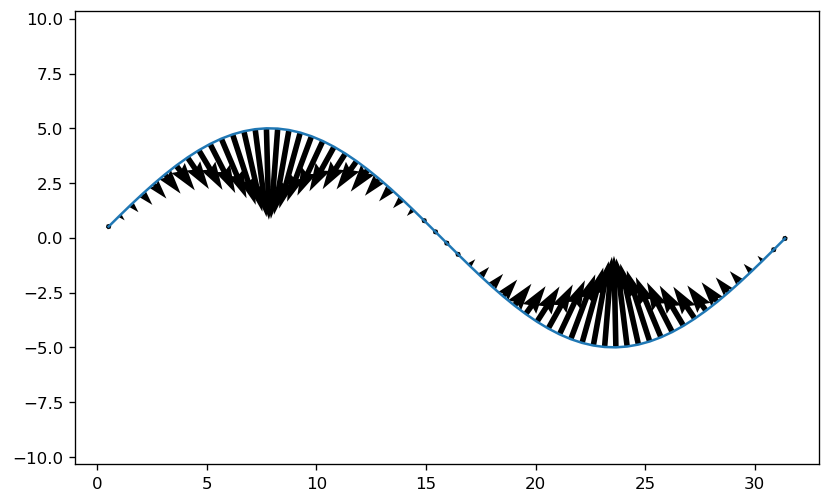
黑尖尖越长,表明该点的曲率越大
曲率半径又是什么意思呢?它等于曲率的倒数:
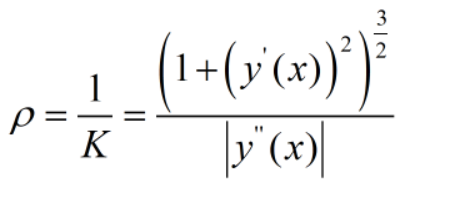
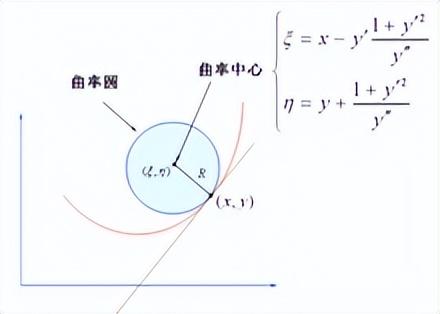
曲率圆越大,曲率半径越大,曲率反而越小,那一点处越不显得“弯”。
还是老办法,讲了这么多不管用的,我还是给大家做个实验让大家“看”见数学吧:现在我们研究一下y=x^2这条抛物线在各点处的曲率是如何变化的。
若:

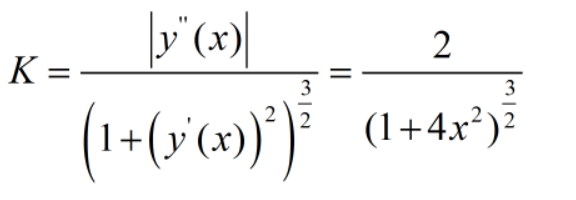
这个曲率图像长什么样子呢?笔者用数学软件给大家画出来了:
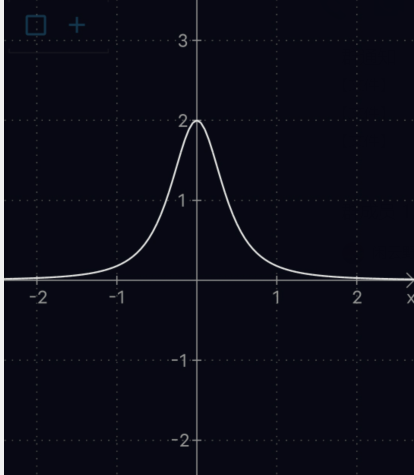
这就是y=x^2的曲率变化,我们发现,它在x=0的时候曲率是最大的,曲率的值是2,之后两边的曲率就越来越小了,曲率越小,长得越像直线。曲率越大,长得越像圆。

哦,多么有趣的问题,曲率越大的东西“长得越圆,越弯”,那么圆的曲率是多少呢?
没错,你没有看错,圆的曲率就是它本身的半径R分之一:
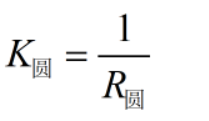

半径越大的圆,它的曲率越小,是不是很奇怪呢?